Student Problem 5

This shows how to solve a partial fraction decomposition with distinct factors. You need to make sure to factor out completely and get the least common denominator for the 2 fractions. Also, don't forget to set the coefficients of the numerator equal to the like terms. If a coefficient is missing, set it equal to zero. The final step is to solve for a factor using substitution and don't forget to plug back in to get the other factors. Plug A,B,C back over the split up fractions.

Student Problem 6

This problem shows you how to do partial fraction decomposition with repeated factors. 

You need to remember to count the powers since we have repeated factors. 

Extra Haiku

Homework
Classwork
Work piles
Too much work
Junior year is very stressful
Cannot wait to graduate and hopefully attend USC

Extra Haiku

Sports
Football
Segerstrom Football
I love it
I have played for years
Football is more than a hobby to me

Wpp #10

Create your own Playlist on MentorMob!

WPP#9

Create your own Playlist on MentorMob!

Fibonacci Haiku

Fibonacci's
Number
Fibonacci's Number
The Golden Ratio
Divide term by preceeding term
Oh! Oh! Oh! Thats What Makes You Beautiful!

Student Problem 7

This shows how to write a repeating decimal as a rational number using geometric series. The first step is to group the irrational number into 3 pairs. You need to separate the number into a group of 2, a group of 4, and a group of 6. . This is shown with the brackets in the picture below. Once you do this you write your pairs in a sequence. You need to make sure to replace the first two numbers of the group of 4 with 2 zeros. You also need to replace the first four numbers of the group of 6 with 4 zeros. 

Once you have done this, you determine the first term and the ratio. You find the ratio by dividing any term by the term before it. Once you find your first term and ratio, you can plug them into the infinite geometric sum formula. This is the a(1)/ 1-r. Once you do this you solve. You need to remember when you divide a fraction by a fraction, you get the reciprocal of the second fraction and multiply. Once you do this, the 100's should cancel and you are left with a fraction. You need to make sure to simplify your answer if possible. 

WPP#8

Create your own Playlist on MentorMob!

WPP # 7

Create your own Playlist on MentorMob!

Student Problem 3

Student Problem 3

This problem shows how graph exponential functions as well as finding x and y intercepts, asymptotes, domain and range. My problem was y=3*4^(x-2) - 2 . Students should pay close attention to the a value to determine if their graph will be above or below the asymptote. 

Student Problem # 2

Student Problem #2

This is an example of graphing logarithmic functions and indentifying x intercepts, y intercepts, asymptote, domain, and range. My equation for this example is : f(x)=log3 (x+4) - 2.

Unit H Student Video #3

Undefined y value

6. If the y value is undefined when plugged into the original equation we find the place of the hole a different way. When the y value is undefined we refer to this as indeterminate form. So when the y value is indeterminate, we then plug in our x values into our simplified equation to find the place of the hole. We then solve and find the y point to place the hole.

Differnece of Hole and Vertical Asymptote

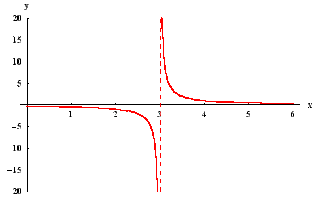
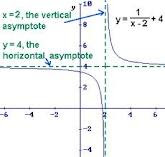
4. Their are several differences of a vertical asymptote and a hole. A vertical asymptote is a line that a graph cannot cross. Vertical asymptotes are written as x=#. Holes are points on a graph where the graph discontinues. Vertical asymptotes coexist with holes because in vertical asymptotes you factor and cross of any common factors. Similarly, holes are points that come from crossed out common factors.

Range of a Rational Function

10. The domain of a rational function depends on DIVAH.  The range of a rational function depends on RIHAH. This means Range is horizontal asymptote holes. The holes of a horizontal asymptote are the points where the graph does not continue and stops and discontinues at that point.

Limit Notation of Vertical Asymptotes

7. To write limit notation for vertical asymptotes, you write as x approches __ (enter x value) and determine if its left or right (with a small negative sign represting left and a plus sign representing right side ) , f(x) approaches (infinity/negative infinity). This means that as x goes either to the right or the left, the graph either goes up or down.

Knowing when a graph has a Slant Asymptote

3. A graph has a slant asymptote only if the degree on top is one bigger than the degree on the bottom. To find the equation of a slant asymptote you divide the top function by the bottom function. This will most likely be done using long division. Everything but your remainder is the equation of the slant asymptote.  The equation should be in Y=mx+b formula.

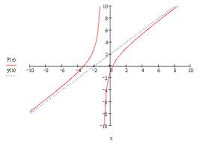
Limit Notation of Horizontal Asymptotes

 2. Limit notation for a horizontal asymptote actually means as the graph either approaches the left or right side of the graph, it also approaches the y value. Limit notation for a horizontal asymptote is written as x approaches either positive or negative infinity, f(x) approaches the y value. 

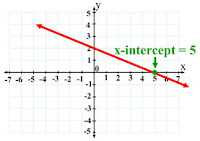
Finding the X Intercepts

9. To find the x intercepts of a rational function, plug in zero for y. This has to be done in the factored equation. Their is a long way and a short way to find the x intercepts. The long method includes multiplying the rational function by the denominator to cancel it. After canceling the denominator you then set the remainig equation equal to 0. The short method includes skipping canceling the denominator and just setting the top equation to 0. This makes mathematical sense because we were going to cancel the denominator anyways, so ignoring this extra step and just setting the top equation to 0 is the same thing. 

STUDENT VIDEO #1: Unit F Concept 10

• What is this video about?
• This video covers a problem from unit f concept 10. This video is about finding all zeroes, real and imaginary, for a 4th or 5th degree polynomial. It walks you through the steps of finding the real and imaginary zeroes. It goes over concepts of p's and q's, descartes rule, and finding zero heroes. 
• What does the viewer need to pay special attention to in order to understand the concept?
• The viewer needs to pay special attention to descartes rule and also which numbers to choose when trying to find a zero heroe. 

Finding the Y-intercept

8. To find the y intercept of a rational function, plug in zero for all the x values and solve. This has to be done in the simplified form. To get the simplified form of the rational function, factor it out, and cancel any similar terms.  After you plug in 0 for all x values, you will either have one or no y intercept.

Knowing if a graph has a Horizontal Asymptote

1. You know a graph has a horizontal asymptote by comparing the degrees of the numerator and denominator. Their are three cases : when their is a bigger degree on top, if the degrees are the same, or if their is a bigger degree on bottom. When the degree is bigger on bottom, the asymptote is y=0. When the degrees are the same, the asymptote is the ratio of the coefficients. When the degree is bigger on top, their is no horizontal asymptote.

Crossing Through an Asymptote

5. A graph can cross through an asymptote under certain conditions. It can cross through a horizontal and slant asymptote only towards the middle of the graph. It can never cross towards the far left or far right. On the other hand, graphs can never cross through a vertical asymptote.