Answer: The mathematical definition of a parabola is that the distance from the focus to any point on the parabola will be the same as it goes straight down perpendicular to the directrix. Because the distance from the focus to any point on the parabola is the same, it creates sets of points that creates a "U" shape which is symmetrically cut in half by the axis of symmetry. 2.How does the focus (or foci) affect the shape of the conic section? (If you choose ellipses, you should include information about eccentricity in your response; if you choose parabolas, "p" should be a big focus... haha, get it? "p" is the distance from vertex to focus and it should be a big focus. Ok, moving on...)
Answer: In a parabola "P" is the distance from the focus to vertex and the vertex to the directrix. The greater the value of "P", the wider the parabola will be. The smaller the value of "P", the skinnier a parabola will be. This is because the greater the value of "P", means that their is a greater distance from the focus to vertex and vertex to directrix. Because each point on a parabola is the same distance from the focus, as p increases, the farther out the points are and so the the parabola is wider. The smaller the value of "P", the smaller the distance from the focus to vertex and vertex to directrix. So the smaller the distance from the focus to points on a parabola , the skinnier a parabola is.
3.How do the properties of this conic section apply in real life? (While using the exact examples I gave you may be acceptable, I will be looking for some research, creativity, and thought. There is a lot out there!
Answer: The properties of Parabolas apply to real life in a automobile headlight. The light from a bulb at the focus point of the metal back of the headlight reflects and is sent outward to light our way in the dark. Also, cable TV dishes are shaped like a parabola. Their shape allows them to absorb parallel waves and reflect them to a specific point (focus). A TV dish is like a parabola because it absorbs the satellite waves and focusses them on a certain point to allow someone to receive a strong enough signal to watch television.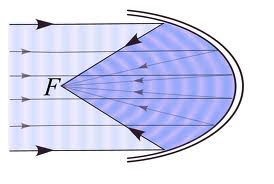 
Citations:
Parabola Image pasted from: http://www.mathsisfun.com/geometry/parabola.html
Focus image paste from http://en.wikipedia.org/wiki/File:Parabolic_reflection_1.svg
Direct tv image from http://www.post-gazette.com/stories/business/news/shopsmart-sorting-out-cable-satellite-phone-web-bundles-377744/
Information from http://www.intmath.com/plane-analytic-geometry/4-parabola.php
